Regularization In Machine learning
Overfitting is a common challenge in machine learning, where a model learns the training data too precisely — including noise and outliers — and fails to perform well on new data. Regularization is a powerful technique designed to prevent overfitting by adding a penalty to the model’s complexity, encouraging it to focus on the most relevant patterns rather than memorizing the data. This helps create models that generalize better to unseen data.
What is Regularization?
Regularization is a method of improving a model's performance on new data by adding a penalty term to the loss function during training. In a standard machine learning model, the loss function measures the difference between predicted values and actual values. Regularization introduces an additional term that discourages large model weights, helping to simplify the model and improve its generalization ability.
Regularized Loss Function:
Loss = Original Loss+ λ × Regularization Term
Where:
Original Loss – Measures the difference between the model’s predictions and the actual target values.
Regularization Term – Adds a penalty for large weights, helping to control model complexity.
λ (lambda) – A hyperparameter that determines the strength of the regularization. Higher λ values increase the penalty, leading to simpler models.
By minimizing this modified loss function, the model becomes less sensitive to noise and better at handling new data.
Types of Regularization
There are two widely used regularization techniques: L1 Regularization and L2 Regularization. They differ in how they apply penalties to the model’s weights.
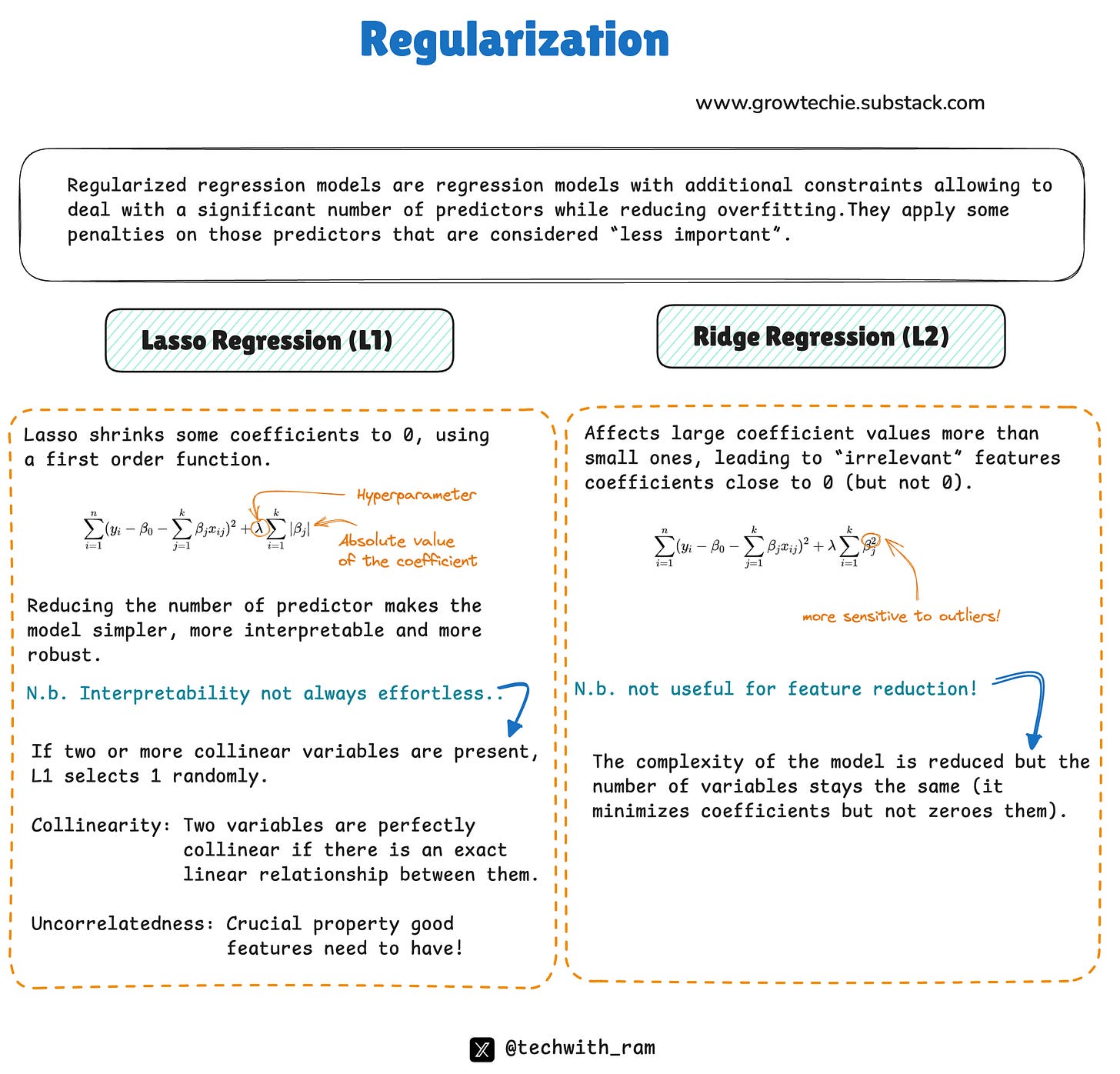
1. L1 Regularization (Lasso Regression)
L1 regularization adds the absolute value of the weights to the loss function:
Loss = Original Loss + λ ∑i∣Wi∣
L1 regularization tends to reduce some weights to exactly zero, effectively removing less important features from the model.
It promotes sparsity — the model focuses only on the most significant features, which makes it useful for feature selection.
Example:
If you're building a house price prediction model, L1 regularization can eliminate the influence of less important features, such as whether the house has a swimming pool, by reducing their corresponding weights to zero. This leads to a simpler model that focuses on the key factors like size and location.
2. L2 Regularization (Ridge Regression)
L2 regularization adds the square of the weights to the loss function:
Loss = Original Loss + λ ∑i Wi^2
L2 regularization reduces all weights proportionally, rather than setting some to zero.
It encourages the model to distribute weight more evenly across features, preventing any single feature from dominating the predictions.
Example:
In the house price prediction scenario, L2 regularization would prevent the model from placing too much importance on a specific feature, like the presence of a swimming pool, ensuring that all factors like size, number of rooms, and location contribute more evenly.
How Regularization Improves Model Performance
Without regularization, a model might assign excessive importance to certain features, which can lead to poor performance on new data. This is especially true if the training data contains outliers or noisy patterns.
Regularization helps by:
- Preventing overfitting by controlling model complexity.
- Improving generalization to new data.
- Reducing the impact of irrelevant or noisy features.
-Creating more interpretable models by simplifying them.
Regularization is an essential tool in machine learning for preventing overfitting and improving model performance on unseen data. L1 regularization (Lasso) is effective for feature selection, while L2 regularization (Ridge) helps balance the contribution of all features. Understanding when and how to use each type of regularization can significantly enhance the accuracy and reliability of your machine learning models.
Twitter: @techwith_ram
Linkedin: @ramakrushnamohapatra