Logistic Regression In Machine Learning

What is Logistic Regression?

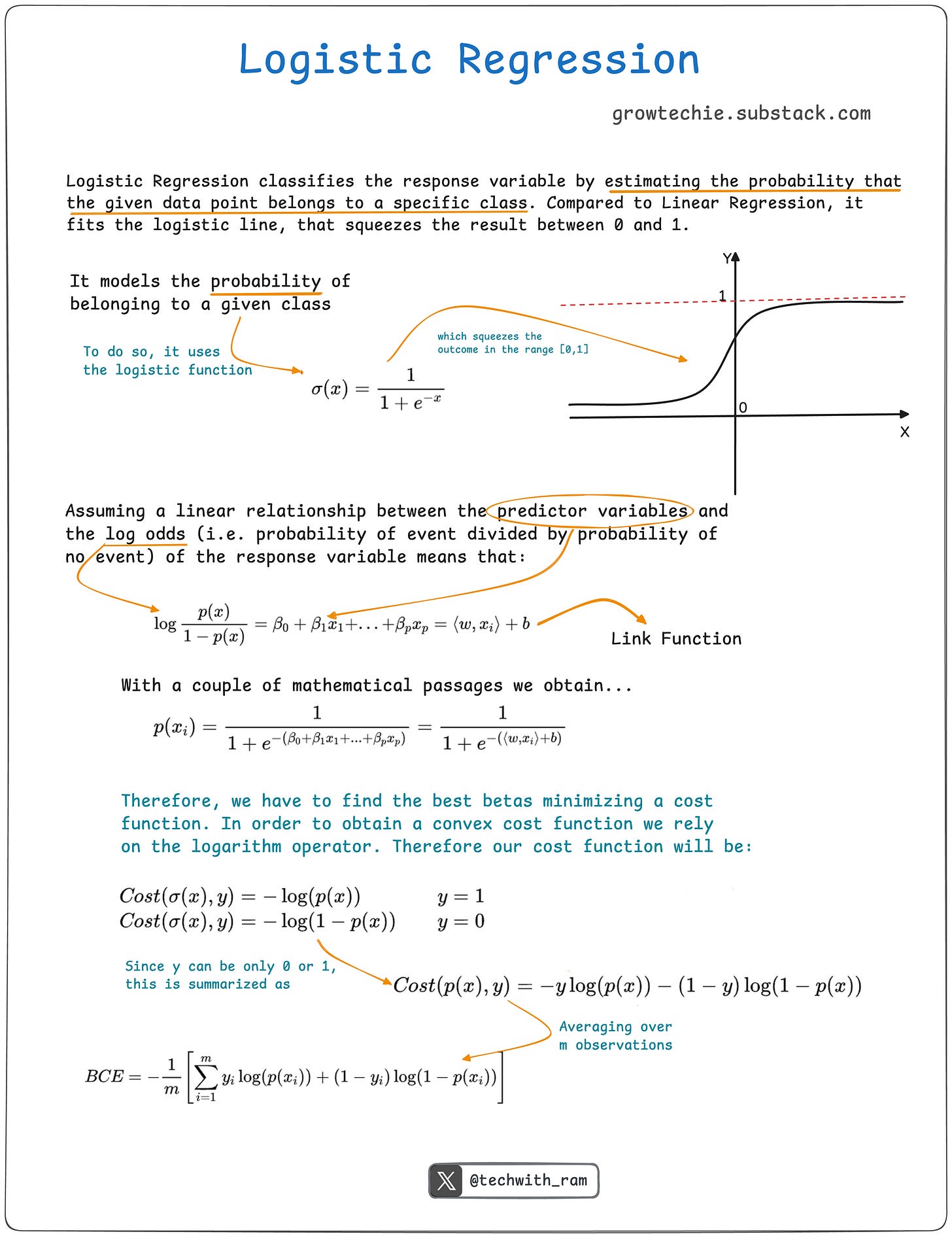
Logistic regression is a machine learning method used for binary classification, where the target variable has two possible outcomes. It models the relationship between one dependent variable and one or more independent variables (which can be categorical or numerical) using the logistic (sigmoid) function to predict probabilities between 0 and 1.

From a maths point of view the coronavirus number of cases graph looks like a sigmoid function but with y values beyond 1 and y being 0 positive for x=0 as if it starts only for positive x values or number of days since the infection.

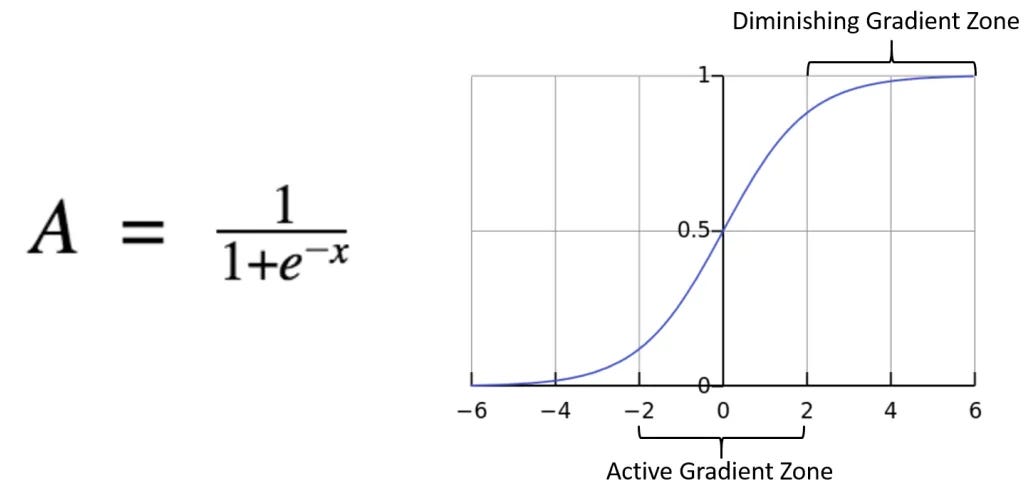
Classic sigmoid function:

Types of Logistic Regression

Logistic regression is a widely used machine learning algorithm for both binary and multi-class classification tasks. Depending on the nature of the dependent variable, it can be classified into three main types:

1. Binary Logistic Regression

• The most common type, used when the dependent variable has only two possible outcomes (e.g., 0 or 1, yes or no, pass or fail).

• The logistic function models the probability of an observation belonging to one of the two classes.

• Example: Predicting whether a customer will buy a product (yes/no).

2. Multinomial Logistic Regression

• Used when the dependent variable has more than two unordered categories.

• Unlike binary logistic regression, it handles multiple classes using the softmax function to ensure the predicted probabilities sum to one.

• Example: Predicting the type of cuisine a person prefers (Italian, Chinese, Indian).

3. Ordinal Logistic Regression

• Applied when the dependent variable has more than two ordered categories with a natural ranking.

• Uses the cumulative logistic distribution function to model cumulative probabilities.

• Example: Customer satisfaction levels (low, medium, high).

Assumptions of Logistic Regression

To ensure the model performs accurately, the following assumptions must hold:
→ The dependent variable should be binary (for binary logistic regression).
→ One level of the dependent variable should represent the desired outcome.
→ Only relevant and meaningful variables should be included.
→ Independent variables should be independent of each other (low multicollinearity).
→ Independent variables should be linearly related to the log odds.
→ A sufficiently large sample size is required for reliable model estimation.

Implementation Using Python

import seaborn as sns
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris

# Load the iris dataset from scikit-learn
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['species'] = iris.target_names[iris.target]
df.head()

df['species'].unique()

df.isnull().sum()

# replace setosa
df=df[df['species']!='setosa']

df['species']=df['species'].map({'versicolor':0,'virginica':1})

# Split dataset into independent and dependent features
X=df.iloc[:,:-1]
y=df.iloc[:,-1]

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=42)

from sklearn.linear_model import LogisticRegression
classifier=LogisticRegression()

# GridSearchCV
from sklearn.model_selection import GridSearchCV
parameter={'penalty':['l1','l2','elasticnet'],'C':[1,2,3,4,5,6,10,20,30,40,50],'max_iter':[100,200,300]}

classifier_regressor=GridSearchCV(classifier,param_grid=parameter,scoring='accuracy',cv=5)

classifier_regressor.fit(X_train,y_train)

#best combination find
print(classifier_regressor.best_params_)

print(classifier_regressor.best_score_)

#prediction
y_pred=classifier_regressor.predict(X_test)

# accuracy score
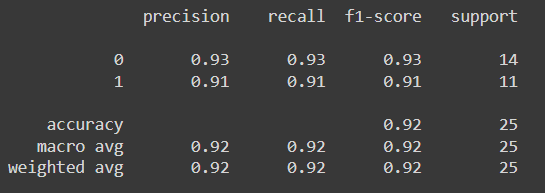
from sklearn.metrics import accuracy_score,classification_report

score=accuracy_score(y_pred,y_test)
print(score)

0.92

print(classification_report(y_pred,y_test))

print(classification_report(y_pred,y_test))

I hope this gives you a comprehensive understanding of logistic regression, from the mathematical intuition with Practical Implementation in Python.

Follow me on socials:

Twitter: @techwith_ram

Linkedin: @ramakrushnamohapatra

---

---

---